Can Loss Mitigation Be A Return Enhancer?
How to get Long Volatility exposure in your balanced portfolio
I came across a post by Convex Strategies, a Singapore-based fund manager that I wasn’t really aware of, that I found really thought provoking. I probably should have been aware of them, because based on the media tab on their website, their CIO is a regular on the podcast circuit. Having been heads-down in the woods for the past fifteen years, I’ve missed some developments in the larger finance world.
Convex Strategies | Risk Update: May2025 – “Just Do It”
The post is about constructing a “make hay while the sun shines” portfolio; not timing the market, but making the most of your time in the market. As you could probably guess from their name, they believe in constructing convex portfolios — portfolios that run to the upside and have their downside capped.
Before going into what the fund manager has to say about portfolio construction, it might be useful to have a quick glossary of terms.
Portfolio Convexity - This is a conceptual term that you might not be able to understand just by Googling, as it’s not Finance SEO Optimized. There is a standard finance term called Convexity that means how the duration of a bond changes as the interest rate changes (the duration being how the price changes as the interest rate changes, so this is the second derivative). This is not that; most searching will just lead you to the bond concept, however. If anything, the way we are using it here is most similar to the concept of gamma with regard to options.
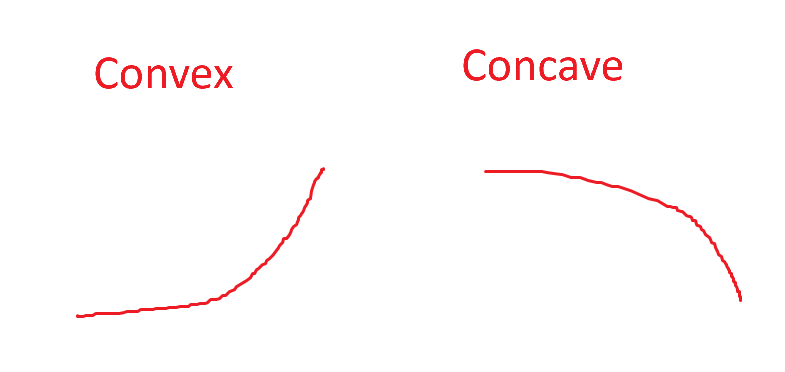
I don’t remember where I first learned about the difference between convex and concave — I’m just talking about the general terms now — but one is a smile and one is a frown.
There are all sorts of mathematical explanations we could go into for how this works in portfolio construction, but in common sense terms, the convex portfolio has small losses and big gains (positive skew, high kurtosis) and the concave portfolio has small gains and big losses (negative skew, high kurtosis).
Volatility - Volatility is just the variation of returns around the average. Practically speaking, though, it means the amount an asset goes up and down. Something that is up 1% one day and down 1% the next day is less volatile than something that goes up 5% one day and down 5% the next (the second asset experiences more volatility). Volatility is a symmetrical term — mathematically speaking, going up a lot counts just as much as going down a lot — but the volatility most market practicioners care about is the volatility to the downside.
Short Volatility, or Selling Vol - This is both a literal strategy that some market players engage in as well as a type of market exposure. On the literal strategy piece, this is a type of investing that pays a little when markets are calm and punishes heavily when markets are highly volatile. A simple option selling strategy is one example of this — you collect a small return when everything goes your way but face nearly unlimited loss when things don’t.
This is also a type of market exposure because that concept of “you collect a small return when everything goes your way but face nearly unlimited loss when things don’t” is basically how most portfolios are constructed. All those things you may have heard about “in a crisis all correlations go to 1” are about this. For this reason, being long assets is basically the same as being short volatility; for the most part, your portfolio generally gains value in calm, low-volatility markets.
Long Volatility, or Buying Vol - This is also both a literal strategy that some market players engage in as well as a type of market exposure. It’s the opposite of the one we just talked about. People usually sound really smart when they talk about it, because it makes a lot of sense — you pay a small fee when markets are calm but can receive massive gains when they’re not. The problem with a strategy like this is that markets are mostly calm most of the time; a simple option buying strategy — the flip of the diagram above — has a negative expected return over time. The ideal way to be long volatility, then, is in a way that makes some money when markets are calm, but makes a lot of money when markets are not. Easier said than done.
Ok, that’s enough of the glossary for now. For those who already knew all this, I’m sorry to waste your time. To those who still don’t understand, it’s tough, I know. Feel free to leave comments about things you’d like to explore in more detail.
Anyway, getting back to constructing convex portfolios: this all sounds great, but like anything, the devil is in the details. They advocate adding strategies that give you long volatility exposure to your baseline portfolio — they assume a 60/40 (60% equities, 40% bonds) portfolio, but the theory holds for any strategic asset allocation — because this strategy will perform well while the rest of your portfolio performs poorly. The strategies they consider are shown in the graphics below.
As you can see, there are only a few strategies that are up when the stock market is down (dark blue bar in Figure 9); crucially, they are also likely delivering some positive return when the rest of the portfolio is up as well. Or, at least, they are not acting as too much of a drag.
This is important because it stands in contrast to a very direct way of being long volatility — buying volatility. Buying options, which is one form of doing this, would add the desired portfolio convexity, but at the cost of constantly paying the option premiums. These premiums act as a drag on returns during calm markets (see glossary on Long Volatility above).
We’re already pushing the limit of my self-imposed “every post should take 1 minute to read” rule, so I’m going to stop here for today. We haven’t accomplished much in terms of constructing a convex portfolio, at least not so far. It certainly looks like there are some types of strategies you can add to your portfolio that will make it more convex, but we haven’t seen how that will work at all. Before we go into that, however, we’re going to have to take a slight detour into something called The Total Portfolio Approach. These questions—and many others—will be answered in the next episode.